3.2.11
Gremlin’s Anatomy
 The Gremlin language is typically described by the individual
steps that make up the language, but it
is worth taking a look at the component parts of Gremlin that make a traversal work. Understanding these component
parts make it possible to discuss and understand more advanced Gremlin topics, such as
Gremlin DSL development and Gremlin debugging techniques.
Ultimately, Gremlin’s Anatomy provides a foundational understanding for helping to read and follow Gremlin of arbitrary
complexity, which will lead you to more easily identify traversal patterns and thus enable you to craft better
traversals of your own.
The Gremlin language is typically described by the individual
steps that make up the language, but it
is worth taking a look at the component parts of Gremlin that make a traversal work. Understanding these component
parts make it possible to discuss and understand more advanced Gremlin topics, such as
Gremlin DSL development and Gremlin debugging techniques.
Ultimately, Gremlin’s Anatomy provides a foundational understanding for helping to read and follow Gremlin of arbitrary
complexity, which will lead you to more easily identify traversal patterns and thus enable you to craft better
traversals of your own.
|
Note
|
This tutorial is based on Stephen Mallette’s presentation on Gremlin’s Anatomy - the slides for that presentation can be found here. |
The component parts of a Gremlin traversal can be all be identified from the following code:
gremlin> g.V().
has('person', 'name', within('marko', 'josh')).
outE().
groupCount().
by(label()).next()
==>created=3
==>knows=2In plain English, this traversal requests an out-edge label distribution for "marko" and "josh". The following sections, will pick this traversal apart to show each component part and discuss it in some detail.
GraphTraversalSource
`g.V()` - You are likely well acquainted with this bit of Gremlin. It is in virtually every traversal you read in documentation, blog posts, or examples and is likely the start of most every traversal you will write in your own applications.
gremlin> g.V()
==>v[1]
==>v[2]
==>v[3]
==>v[4]
==>v[5]
==>v[6]While it is well known that g.V() returns a list of all the vertices in the graph, the technical underpinnings of
this ubiquitous statement may be less so well established. First of all, the g is a variable. It could have been
x, y or anything else, but by convention, you will normally see g. This g is a GraphTraversalSource
and it spawns GraphTraversal instances with start steps. V() is one such start step, but there are others like
E for getting all the edges in the graph. The important part is that these start steps begin the traversal.
In addition to exposing the available start steps, the GraphTraversalSource also holds configuration options (perhaps
think of them as pre-instructions for Gremlin) to be used for the traversal execution. The methods that allow you to
set these configurations are prefixed by the word "with". Here are a few examples to consider:
g.withStrategies(SubgraphStrategy.build().vertices(hasLabel('person')).create()). //1
V().has('name','marko').out().values('name')
g.withSack(1.0f).V().sack() //2
g.withComputer().V().pageRank() //3-
Define a strategy for the traversal
-
Define an initial sack value
-
Define a GraphComputer to use in conjunction with a
VertexProgramfor OLAP based traversals - for example, see Spark
|
Important
|
How you instantiate the GraphTraversalSource is highly depending on the graph database implementation that
you are using. Typically, they are instantiated from a Graph instance with the traversal() method, but some graph
databases, ones that are managed or "server-oriented", will simply give you a g to work with. Consult the
documentation of your graph database to determine how the GraphTraversalSource is constructed.
|
GraphTraversal
As you now know, a GraphTraversal is spawned from the start steps of a GraphTraversalSource. The GraphTraversal
contain the steps that make up the Gremlin language. Each step returns a GraphTraversal so that the steps can be
chained together in a fluent fashion. Revisiting the example from above:
gremlin> g.V().
has('person', 'name', within('marko', 'josh')).
outE().
groupCount().
by(label()).next()
==>created=3
==>knows=2the GraphTraversal components are represented by the has(), outE() and groupCount()-steps. The key to reading
this Gremlin is to realize that the output of one step becomes the input to the next. Therefore, if you consider the
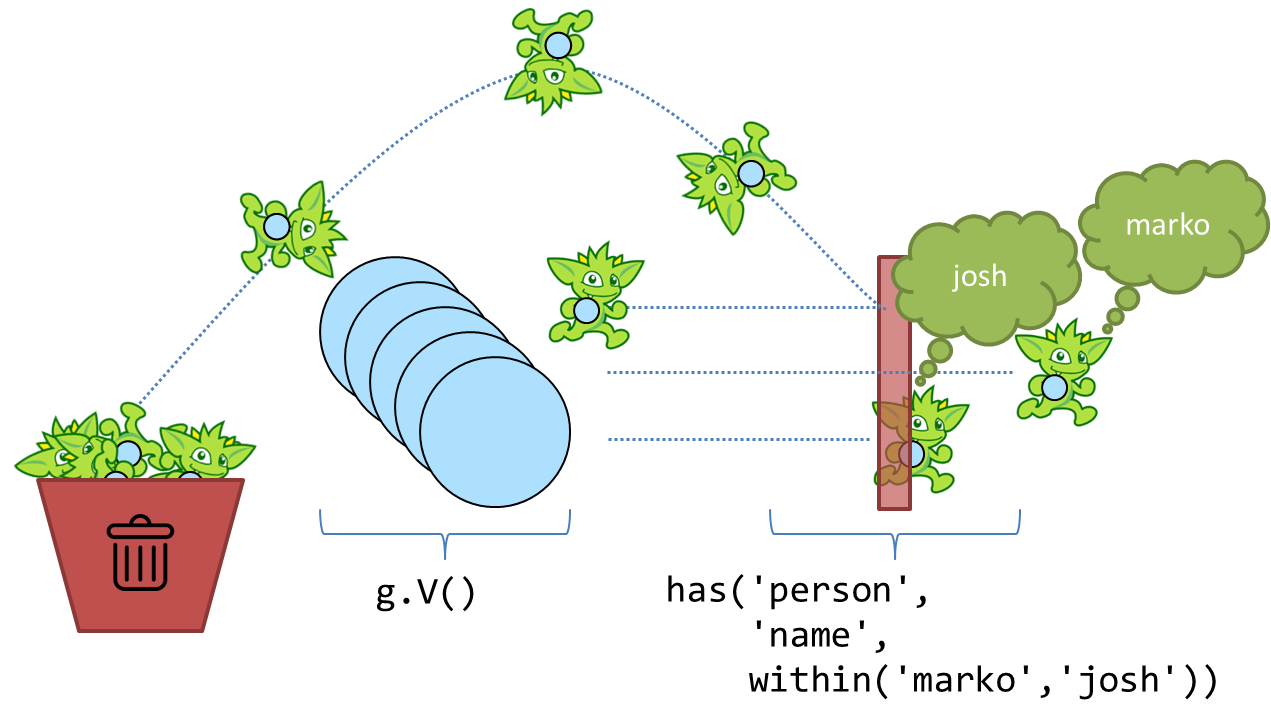
start step of V() and realize that it returns vertices in the graph, the input to has() is going to be a Vertex.
The has()-step is a filtering step and will take the vertices that are passed into it and block any that do not
meet the criteria it has specified. In this case, that means that the output of the has()-step is vertices that have
the label of "person" and the "name" property value of "josh" or "marko".
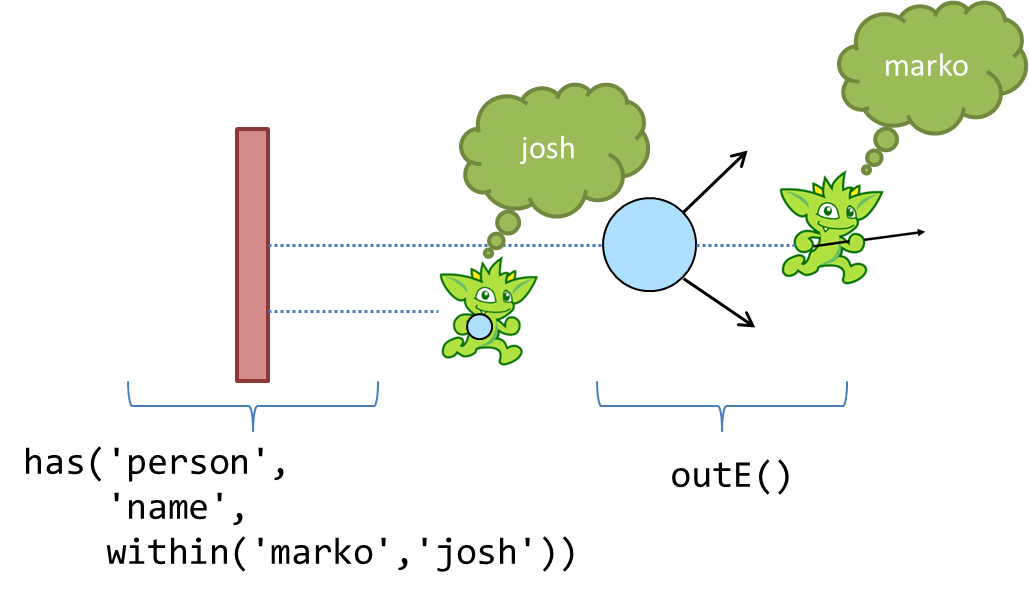
Given that you know the output of has(), you then also know the input to outE(). Recall that outE() is a
navigational step in that it enables movement about the graph. In this case, outE() tells Gremlin to take the
incoming "marko" and "josh" vertices and traverse their outgoing edges as the output.
Now that it is clear that the output of outE() is an edge, you are aware of the input to groupCount() - edges.
The groupCount()-step requires a bit more discussion of other Gremlin components and will thus be examined in the
following sections. At this point, it is simply worth noting that the output of groupCount() is a Map and if a
Gremlin step followed it, the input to that step would therefore be a Map.
The previous paragraph ended with an interesting point, in that it implied that there were no "steps" following
groupCount(). Clearly, groupCount() is not the last function to be called in that Gremlin statement so you might
wonder what the remaining bits are, specifically: by(label()).next(). The following sections will discuss those
remaining pieces.
Step Modulators
It’s been explained in several ways now that the output of one step becomes the input to the next, so surely the Map
produced by groupCount() will feed the by()-step. As alluded to at the end of the previous section, that
expectation is not correct. Technically, by() is not a step. It is a step modulator. A step modulator modifies the
behavior of the previous step. In this case, it is telling Gremlin how the key for the groupCount() should be
determined. Or said another way in the context of the example, it answers this question: What do you want the "marko"
and "josh" edges to be grouped by?
Anonymous Traversals
In this case, the answer to that question is provided by the anonymous traversal label() as the argument to the step
modulator by(). An anonymous traversal is a traversal that is not bound to a GraphTraversalSource. It is
constructed from the double underscore class (i.e. ), which exposes static functions to spawn the anonymous
traversals. Typically, the double underscore is not visible in examples and code as by convention, TinkerPop typically
recommends that the functions of that class be exposed in a standalone fashion. In Java, that would mean
statically importing the
methods, thus allowing .label() to be referred to simply as label().
|
Note
|
In Java, the full package name for the __ is org.apache.tinkerpop.gremlin.process.traversal.dsl.graph.
|
In the context of the example traversal, you can imagine Gremlin getting to the groupCount()-step with a "marko" or
"josh" outgoing edge, checking the by() modulator to see "what to group by", and then putting edges into buckets
by their label() and incrementing a counter on each bucket.
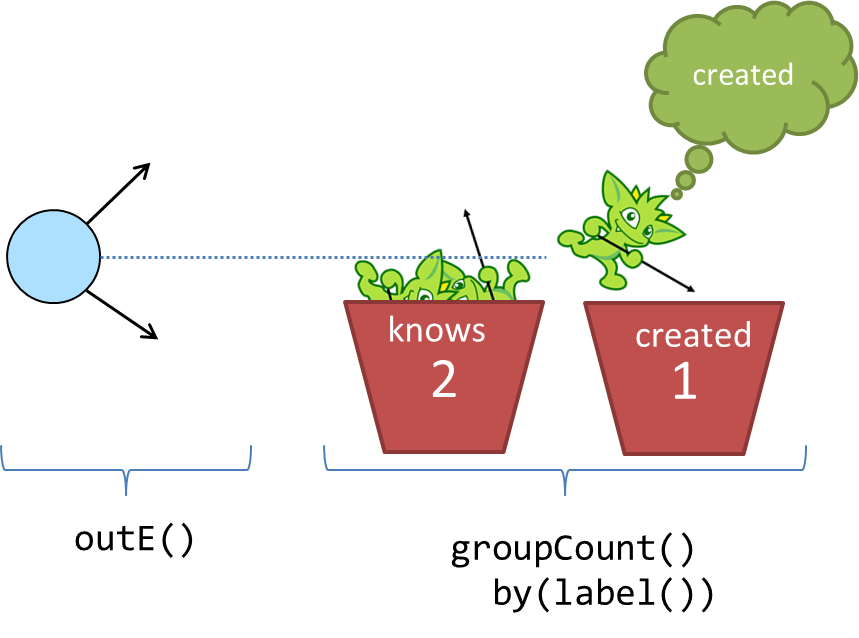
The output is thus an edge label distribution for the outgoing edges of the "marko" and "josh" vertices.
Terminal Step
Terminal steps are different from the GraphTraversal steps in that terminal steps do not return a GraphTraversal
instance, but instead return the result of the GraphTraversal. In the case of the example, next() is the terminal
step and it returns the Map constructed in the groupCount()-step. Other examples of terminal steps include:
hasNext(), toList(), and iterate(). Without terminal steps, you don’t have a result. You only have a
GraphTraversal
|
Note
|
You can read more about traversal iteration in the Gremlin Console Tutorial. |
Expressions
It is worth backing up a moment to re-examine the has()-step. Now that you have come to understand anonymous
traversals, it would be reasonable to make the assumption that the within() argument to has() falls into that
category. It does not. The within() option is not a step either, but instead, something called an expression. An
expression typically refers to anything not mentioned in the previously described Gremlin component categories that
can make Gremlin easier to read, write and maintain. Common examples of expressions would be string tokens, enum
values, and classes with static methods that might spawn certain required values.
A concrete example would be the class from which within() is called - P. The P class spawns Predicate values
that can be used as arguments for certain traversals teps. Another example would be the T enum which provides a type
safe way to reference id and label keys in a traversal. Like anonymous traversals, these classes are usually
statically imported so that instead of having to write P.within(), you can simply write within(), as shown in the
example.
Conclusion
There’s much more to a traversal than just a bunch of steps. Gremlin’s Anatomy puts names to each of these component parts of a traversal and explains how they connect together. Understanding these components part should help provide more insight into how Gremlin works and help you grow in your Gremlin abilities.
